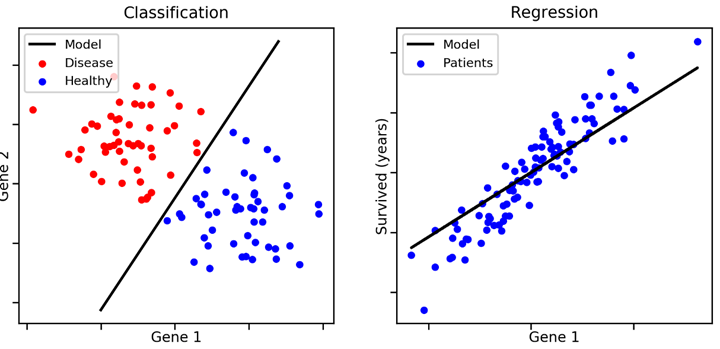
Supervised Learning¶
- Goal
- Given data $X$ in feature sapce and the labels $Y$
- Learn to predict $Y$ from $X$
- Labels could be discrete or continuous
- Continuous-valued labels: Regression
- Discrete-valued labels: Classification - I don't care
Notation¶
In this lecture, we will use
- Data $x \in R^D$ (scalar- or vector-valued)
- Features $\phi(x) \in R^M$ for data $x$
- Continuous-valued labels $t \in R$ (target values)
We will interchangeably use
- $x^{(n)}, x_n$ to denote the $n^\text{th}$ training example.
- $t^{(n)}, t_n$ to denote the $n^\text{th}$ target value.
Linear Regression (1d inputs)¶
- Consider 1d case (e.g. D=1)
- Given a set of observations $x_1, \dots, x_N$
- and corresponding target values $t_1, \dots, t_N$
- We want to learn a function $y(x, \vec{w}) \approx t$ to predict future values.
$$ y(x, \vec{w}) = w_0 + w_1 x + w_2 x^2 + \dots w_M x^M = \sum_{k=0}^M w_k x^k $$
Regression: Noisy Data¶
xx, yy = generateData(100, False) # Truth, without noise
x, y = generateData(13, True) # Noisy observation, training samples
plt.plot(xx, yy, 'g--')
plt.plot(x, y, 'ro');
Regression: 0th Order Polynomial¶
coeffs = np.polyfit(x, y, 0) # Leveraging NumPy's polyfit as short-cut; 0 is the degree of the poly
poly = np.poly1d(coeffs) # Polynomial with "learned" parameters
plt.plot(xx, yy, "g--")
plt.plot(x, y, "ro")
plt.plot(xx, poly(xx), "b-");
Regression: 1st Order Polynomial¶
coeffs = np.polyfit(x, y, 1) # Now let's try degree = 1
poly = np.poly1d(coeffs)
plt.plot(xx, yy, "g--")
plt.plot(x, y, "ro")
plt.plot(xx, poly(xx), "b-");
Regression: 3rd Order Polynomial¶
coeffs = np.polyfit(x, y, 3) # Now degree = 3
poly = np.poly1d(coeffs)
plt.plot(xx, yy, "g--")
plt.plot(x, y, "ro")
plt.plot(xx, poly(xx), "b-");
Linear Regression (General Case)¶
The function $y(\vec{x}, \vec{w})$ is linear in parameters $\vec{w}$.
- Goal: Find the best value for the weights, $\vec{w}$.
- For simplicity, add a bias term $\phi_0(\vec{x}) = 1$.
$$ y(\vec{x}, \vec{w}) = w_0 + \sum_{j=0}^{M-1} w_j \phi_j(\vec{x}) = \vec{w}^T \phi(\vec{x}) $$
Basis Functions¶
The basis functions $\phi_j(\vec{x})$ need not be linear.
r = np.linspace(-1,1,100)
f, axs = plt.subplots(1, 3, figsize=(12,4))
for j in range(8):
axs[0].plot(r, np.power(r,j))
axs[1].plot(r, np.exp( - (r - j/7.0 + 0.5)**2 / 2*5**2 ))
axs[2].plot(r, 1 / (1 + np.exp( - (r - j/5.0 + 0.5) * 5)) )
set_nice_plot_labels(axs)
Least Squares: Objective Function¶
Minimize the residual error over the training data.
$$ E(\vec{w}) = \frac12 \sum_{n=1}^N (y(x_n, \vec{w}) - t_n)^2 = \frac12 \sum_{n=1}^N \left( \sum_{j=0}^{M-1} w_j\phi_j(\vec{x}^{(n)}) - t^{(n)} \right)^2 $$
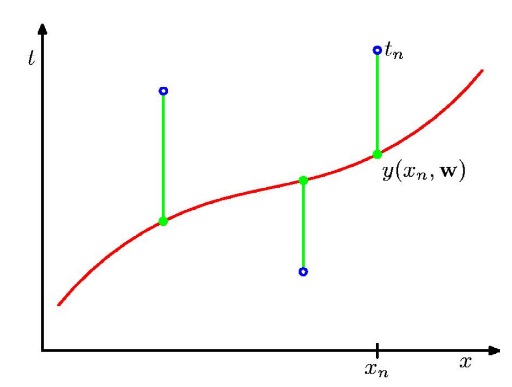
Least Squares: Gradient Calculation¶
Closed Form Solution: Derivation¶
$$ \begin{align} \mbox{Scarlar Form: } E(\vec{w}) &= \frac12 \sum_{n=1}^N \left( \sum_{j=0}^{M-1} w_j \phi_j(\vec{x}^{(n)}) - t^{(n)} \right)^2 \\ &= \frac12 \sum_{n=1}^N \left( \vec{w}^T \phi(\vec{x}^n) - t^{(n)} \right)^2 \\ &= \frac12 \sum_{n=1}^N (\vec{w}^T \phi( \vec{x}^{(n)} ) )^2 - \sum_{n=1}^N t^{(n)} \vec{w}^T \phi( \vec{x}^{(n)} ) + \frac12 \sum_{n=1}^N (t^{(n)})^2 \\ \mbox{Vector Form: } E(\vec{w}) &= \frac12 \|\Phi \vec{w} - \vec{t}\|^2 \\ &= \frac12 \vec{w}^T \Phi^T \Phi \vec{w} - \vec{w}^T \Phi^T \vec{t} + \frac12 \vec{t}^T \vec{t} \end{align}$$
Closed Form Solution: Data Matrix¶
The design matrix is a matrix $\Phi \in R^{N \times M}$, applying
- the $M$ basis functions (columns)
- to $N$ data points (rows)
$$ \Phi = \begin{bmatrix} \phi_0(\vec{x}_1) & \phi_1(\vec{x}_1) & \cdots & \phi_{M-1}(\vec{x}_1) \\ \phi_0(\vec{x}_2) & \phi_1(\vec{x}_2) & \cdots & \phi_{M-1}(\vec{x}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(\vec{x}_N) & \phi_1(\vec{x}_N) & \cdots & \phi_{M-1}(\vec{x}_N) \\ \end{bmatrix} $$
Goal: $\Phi \vec{w} \approx \vec{t}$
Least Squares: Gradient via Matrix Calculus¶
- Compute the gradient and set to zero
\begin{align} \nabla_\vec{w} E(\vec{w}) &= \nabla_\vec{w} \left[ \frac12 \vec{w}^T \Phi^T \Phi \vec{w} - \vec{w}^T \Phi^T \vec{t} + \frac12 \vec{t}^T \vec{t} \right] \\ &= \Phi^T \Phi \vec{w} - \Phi^T \vec{t} = 0 \end{align}
- Solve the resulting normal equation: $$ \Phi^T \Phi \vec{w} = \Phi^T \vec{t},\quad \vec{w} = (\Phi^T \Phi)^{-1} \Phi^T \vec{t} $$
This is the Moore-Penrose pseudoinverse, $\Phi^\dagger = (\Phi^T \Phi)^{-1} \Phi^T$ applied to solve the linear system $\Phi \vec{w} \approx \vec{t}$.
Digression: Moore-Penrose Pseudoinverse¶
- When we have a matrix $A$ that is non-invertible or not even square, we might want to invert anyway
- For these situations we use $A^\dagger$, the Moore-Penrose Pseudoinverse of $A$
- When $A$ has lin. indep. columns then $A^\dagger = (A^\top A)^{-1} A^\top$
- In general, we can get $A^\dagger$ by SVD: if we write $A = U \Sigma V^\top$ then $A^\dagger = V \Sigma^\dagger U^\top$, where $\Sigma^\dagger$ is obtained by taking reciprocals of non-zero entries of $\Sigma$.
Alternative View: Projection onto subspace¶
- Columns of $\Phi$ forms a subspace and we are essentially projecting $\vec{t}$ onto $\Phi$ when doing $\Phi \vec{x}=\vec{t}$
- The SVD $\Phi=U\Sigma V^T$ produces the orthonormal basis $U$ and transformation matrix $T=\Sigma V^T$
- Recall from review of linear algebra, let $\vec{y}=T\vec{x}$, then $U\vec{y}=\vec{t}$ and $\vec{y}\approx U^T\vec{t}$
- Then $\vec{x}=T^{-1}\vec{y}=V\Sigma^\dagger U^T \vec{t}=\Phi^\dagger \vec{t}$
Detailed derivation - Scalar version - Skip in class¶
Least Squares: Gradient Calculation¶
To minimize the error, take partial derivatives w.r.t. each weight $w_j$:
$$ \frac{\partial E(\vec{w})}{\partial w_k}= \frac{\partial}{\partial w_k} \left[ \frac12 \sum_{n=1}^N \left( \sum_{j=0}^{M-1} w_j\phi_j(\vec{x}^{(n)}) - t^{(n)} \right)^2 \right] $$
Apply the chain rule:
$$ = \sum_{n=1}^N \left[ \left( \sum_{j=0}^{M-1} w_j\phi_j(\vec{x}^{(n)}) - t^{(n)} \right) \frac{\partial}{\partial w_k} \left[ \sum_{j=0}^{M-1} w_j\phi_j(\vec{x}^{(n)}) - t^{(n)} \right] \right] $$
$$ = \sum_{n=1}^N \left[ \left( \sum_{j=0}^{M-1} w_j\phi_j(\vec{x}^{(n)}) - t^{(n)} \right) \phi_k(\vec{x}^{(n)}) \right] $$
Least Squares: Vectorized Gradient¶
$$ \begin{align} \nabla_w E(\vec{w}) &= \sum_{n=1}^N \left( \sum_{j=0}^{M-1} w_j \phi_j(\vec{x}^{(n)}) - t^{(n)} \right) \phi(\vec{x}^{(n)}) \\ &= \sum_{n=1}^N \left( \vec{w}^T \phi(\vec{x}^{(n)}) - t^{(n)} \right) \phi(\vec{x}^{(n)}) \end{align} $$
Closed Form Solution¶
Main Idea: Compute gradient and set to gradient to zero, solving in closed form.
- Objective function: $$E(\vec{w}) = \frac12 \sum_{n=1}^N \left( \sum_{j=0}^{M-1} w_j\phi_j(\vec{x}^{(n)})- t^{(n)}\right)^2$$
- We will derive the gradient using matrix calculus.
Detailed derivation - Matrix Calculus - Skip in class¶
Matrix Calculus: The Gradient¶
Suppose that $f : R^{m \times n} \mapsto R$, that is, the function $f$
- takes as input a matrix $A \in R^{m\times n} = [a_{ij}]$
- returns a real value
Then, the gradient of $f$ with respect to $A$ is:
$$ \nabla_A f(A) \in R^{m \times n} = \begin{bmatrix} % \frac{\partial f}{\partial a_{11}} & \frac{\partial f}{\partial a_{12}} & \cdots & \frac{\partial f}{\partial a_{1n}} \\ % \frac{\partial f}{\partial a_{21}} & \frac{\partial f}{\partial a_{22}} & \cdots & \frac{\partial f}{\partial a_{2n}} \\ % \vdots & \vdots & \ddots & \vdots \\ % \frac{\partial f}{\partial a_{m1}} & \frac{\partial f}{\partial a_{m2}} & \cdots & \frac{\partial f}{\partial a_{mn}} \\ \end{bmatrix},\quad [\nabla_A f(A)]_{ij} = \frac{\partial f}{\partial a_{ij}} $$
Matrix Calculus: The Gradient¶
Note that the size of $\nabla_A f(A)$ is always the same as the size of $A$. In particular, for vectors $x \in R^n$,
$$ \nabla_x f(x) = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \cdots & \frac{\partial f}{\partial x_n} \end{bmatrix}^T $$
The gradient is a linear operator from $R^n \mapsto R^n$:
- $ \nabla_x (f + g) = \nabla_x f + \nabla_x g $
- $ \forall\, c \in R, \nabla_x (c f) = c \nabla_x f$
Gradient: Linear Functions¶
The gradient of the linear function $f(x) = \sum_{k=1}^n b_k x_k = b^T x$ is
$$ \frac{\partial f}{\partial x_k} = \frac{\partial}{\partial x_k} \sum_{k=1}^n b_k x_k = \sum_{k=1}^n \frac{\partial}{\partial x_k} b_k x_k = b_k $$
In a more compact form,
$$ \nabla_x b^T x = b $$
Gradient: Quadratic Forms¶
- Every symmetric $A \in R^{n \times n}$ corresponds to a quadratic form: $$ f(x) = \sum_{i=1}^n \sum_{j=1}^n x_i A_{ij} x_j = x^T A x $$
- The partial derivatives are $$ \frac{\partial f}{\partial x_k} = 2 \sum_{j=1}^n A_{ij} x_j = 2 [Ax]_i $$
- Compact form $\nabla_x f(x) = 2 Ax$
stys = ['k-', 'k-.', 'm-', 'm-.']
plt.plot(xx, yy, "g--")
plt.plot(x, y, "ro", label="Training data")
for _i in range(4):
plt.plot(xx, tsts[_i], stys[_i], label='Order {0}'.format(_i))
plt.legend();
Root of Mean-Squared Error, RMSE¶
$$ E_{RMS} = \sqrt{2E(w^*) / N} = \sqrt{\frac{1}{N}\sum_{i=1}^N[f(x_i)-t_i]^2} $$
- Easy to compute
- Potential issue: Improperly scaled
f, ax = plt.subplots(ncols=4, sharey=True, figsize=(16,4))
for _i in range(4):
ax[_i].plot(xx, yy, "g--")
ax[_i].plot(x, y, "ro")
ax[_i].plot(xx, tsts[_i])
ax[_i].set_title('Order {0}, RMSE={1:4.3f}'.format(_i, es[_i]))
Coefficient of determination¶
$$ R^2 = 1 - \frac{SS_{res}}{SS_{tot}} $$
- Let $\bar{t}$ be average of $\{t_i\}$
- Residual sum of squares: $$SS_{res}=\sum_i[f(x_i)-t_i]^2$$
- Total sum of squares: $$SS_{tot}=\sum_i[t_i-\bar{t}]^2$$
- Explained sum of squares: $$SS_{reg}=\sum_i[f(x_i)-\bar{t}]^2$$
f, ax = plt.subplots(ncols=4, sharey=True, figsize=(16,4))
for _i in range(4):
ax[_i].plot(y, y, "r-")
ax[_i].plot(y, trns[_i], "bo")
ax[_i].set_title('Order {0}, R2={1:4.3f}'.format(_i, rs[_i]))
Geometrical interpretation of R2¶
- Blue: Squared residuals w.r.t. the linear regression.
- Red: Squared residuals w.r.t. the average value.
$$ R^2 = 1 - \frac{\color{blue}{SS_{res}}}{\color{red}{SS_{tot}}} $$