Published: Dec 21, 2025 by Daning Huang
Earlier in the year, we presented an ICLR spotlight paper on learning dynamics on manifold, using a specially designed kernel method. Our recent work superceeds the method using a surprisingly simpler formulation, while extending even to chaotic dynamics, where the states no longer lie on nice smooth objects such as manifolds, but fractal-dimensional strange attractors.
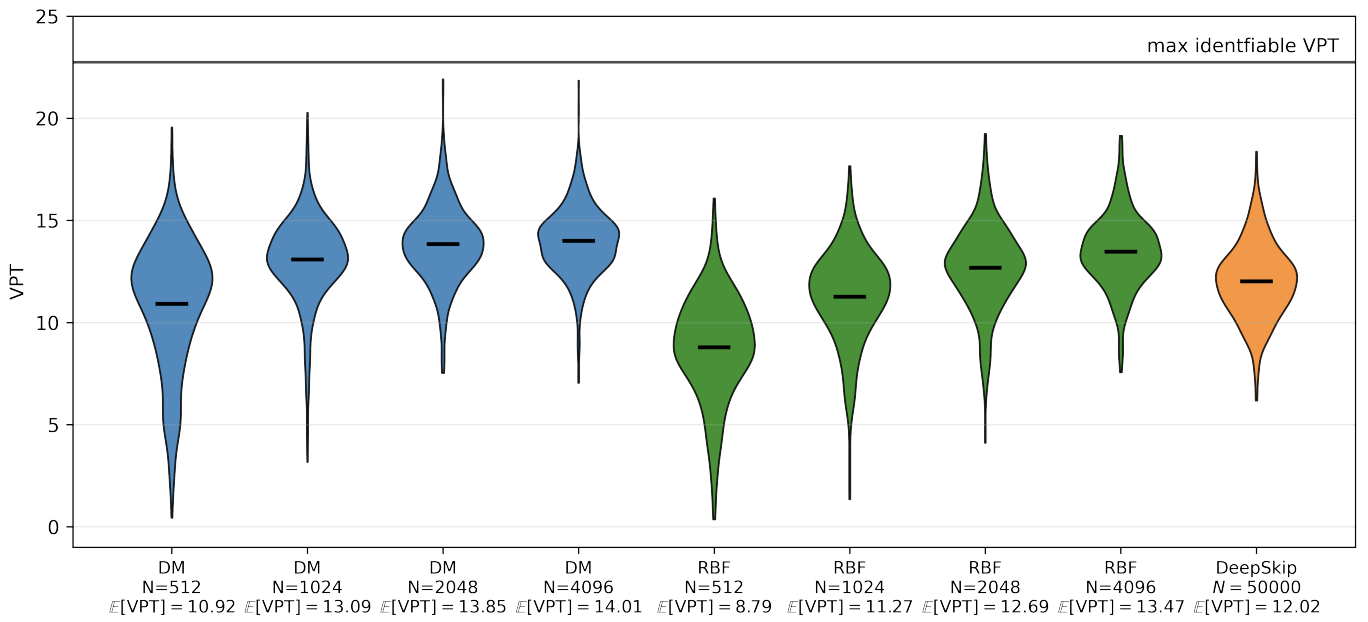
Across a broad range of systems, including smooth manifolds, chaotic attractors, and high-dimensional spatiotemporal flows, the new method, DM-KRR, consistently outperforms stateof-the-art random feature, neural-network and operator-learning methods in both accuracy and data efficiency. These findings underscore that long-term predictive skill depends not only on model expressiveness, but critically on respecting the geometric constraints encoded in the data through dynamically consistent model selection. Together, simplicity, geometry awareness, and strong empirical performance point to a promising path for reliable and efficient learning of complex dynamical systems.
The core functionality of the paper has been implemented in our dynamics learning package, with one example here.
This work is supported by NSF CDSE Program.