Published: Mar 30, 2025 by Daning Huang
For the coming ICLR 2025 conference we are proud to present a Spotlight paper: “Learning vector fields of differential equations on manifolds with geometrically constrained operator-valued kernels”. Only 3.3% papers of the nearly 11500 submissions are selected as Spotlight.
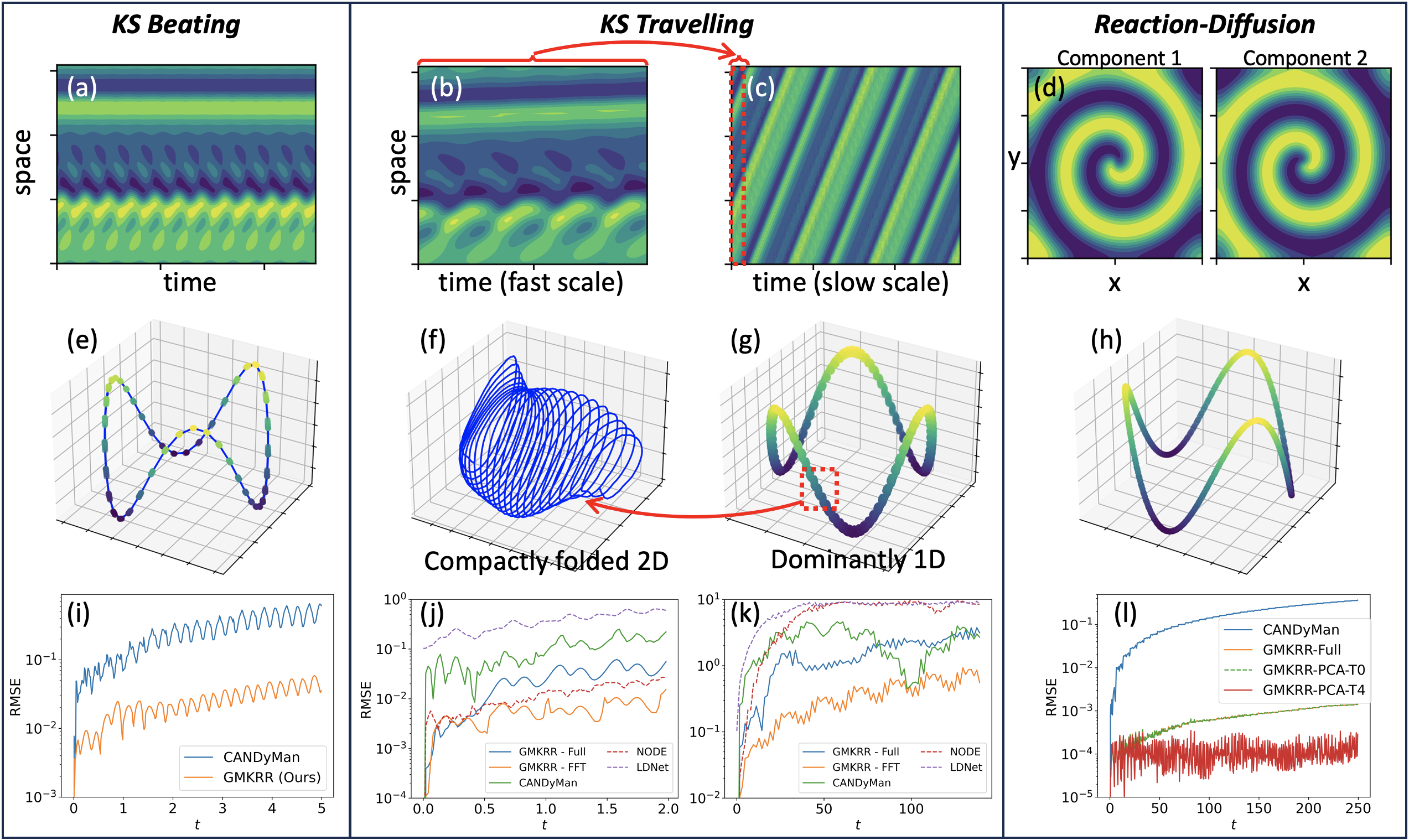
In this work, we address the problem of learning ordinary differential equations (ODEs) on manifolds by devising (1) an operator-valued kernel to represent vector fields on manifolds and (2) a geometry-preserving time integrator that enforces the ODE solution to lie a manifold. The algorithm is rooted in theories of differential goemetry and dynamical systems, with rigorous convergence bounds. We verify the effectiveness of the proposed approach on high-dimensional dynamical systems, including the cavity flow problem, the beating and travelling waves in Kuramoto-Sivashinsky equations, and the reaction-diffusion dynamics.
The work is done jointly with Dr. John Harlim from Math & Meteorology and Dr. Yan Li from EECS at Penn State.
For more details, see paper and code, slides, poster, and 5-min presentation.