Published: Jul 26, 2024 by Daning Huang
Networked systems, i.e., the systems that involve many interacting dynamical components, are universal in engineering; an example is the energy system of an electrified aircraft. Obtaining a dynamic model from the data of such a system has two challenges: (1) the data is unstructured (defined on graph) - this causes difficulties in model representation, and (2) the system is typically stiff due to multiple timescales - this causes difficulties in learning the dynamics.
To overcome the above challenges, in our recent ArXiv manuscript, we developed a weak Latent Dynamics Model (wLDM) for learning possibly stiff nonlinear dynamics with control, and extended the wLDM framework to develop weak Graph Koopman Bilinear Form (wGKBF) model, which integrates geometric deep learning and Koopman theory to learn latent space dynamics for networked systems.
The work is done jointly with Dr. Herschel Pangborn from Mechanical Engineering at Penn State.
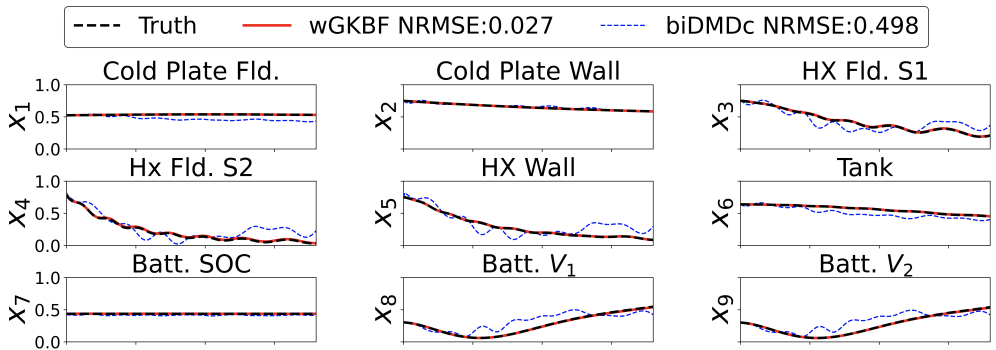
(Figure shows effectiveness of wGKBF model in comparison to the standard biDMD algorithm for an electrified aircraft system.)