Published: Sep 1, 2022 by Daning Huang
Often a complex engineering system can be modeled as a system of subsystems that interact with each other and with the environment. Leveraging the connectivity between the subsystems, i.e., the topology, can greatly reduce the efforts in the modeling, optimization, and control of such systems. The geometric deep learning technique, esp., graph neural networks (GNNs), is an effective and powerful tool for the topology-informed modeling of complex systems, with a few unique features:
- Training efficiency and scalability: The GNNs model localized interactions between the subsystems; thus can be trained on datasets of small systems and scale up to large inter-connected systems
- Missing data completion: The GNNs reconstruct missing dynamical states by leveraging spatiotemporal correlations as well as time-delay embedding theorems in dynamical system theory
Recently, we have been able to apply GNNs for various applications, from the vanilla modeling of dynamics
- Power grid dynamics (Figure left below, paper, fund)
- Ship airwakes (Figure right below, paper)
- Heatwave forecasting (More details, paper)
to the control of inter-connected systems, such as
- Hierarchical control of electrothermal systems (fund)
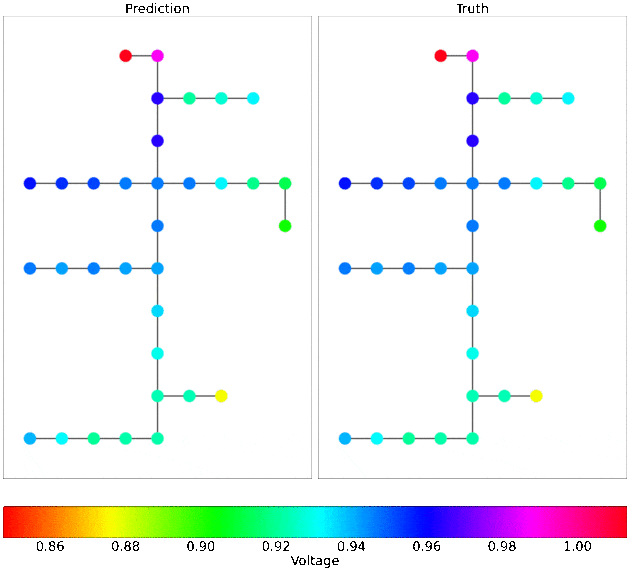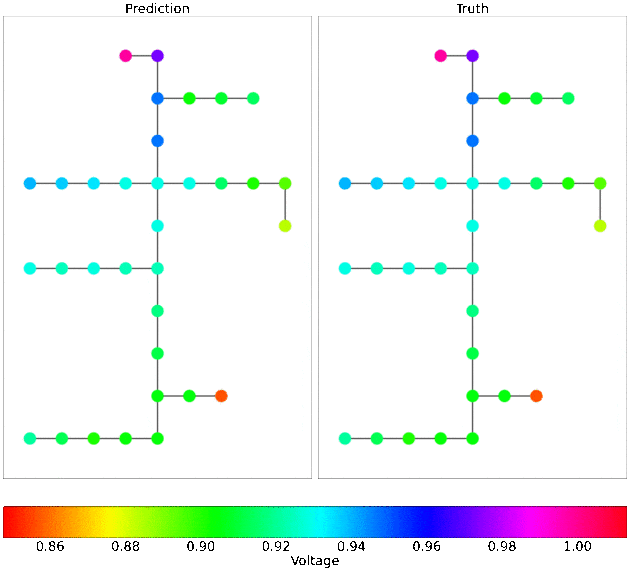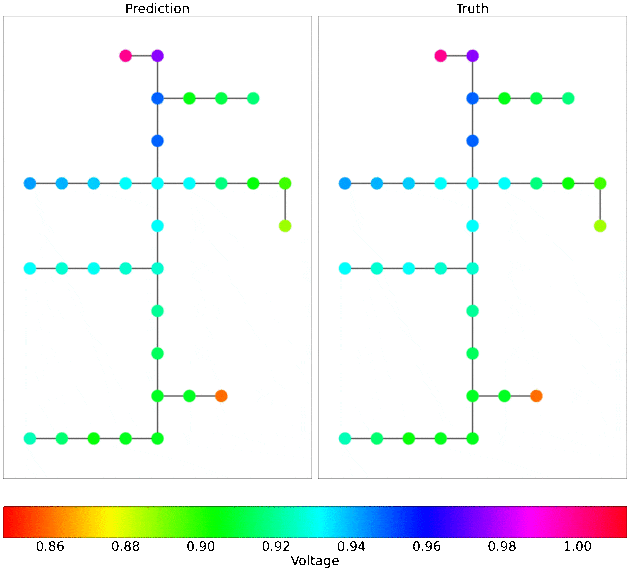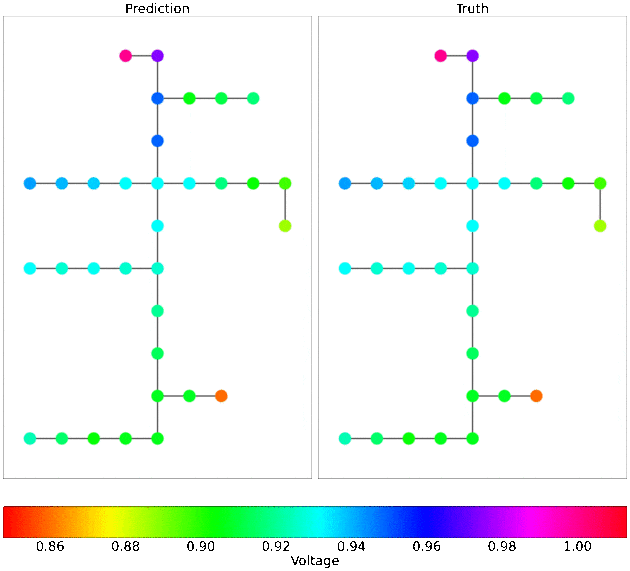 |
 |