Published: Nov 30, 2022 by Daning Huang
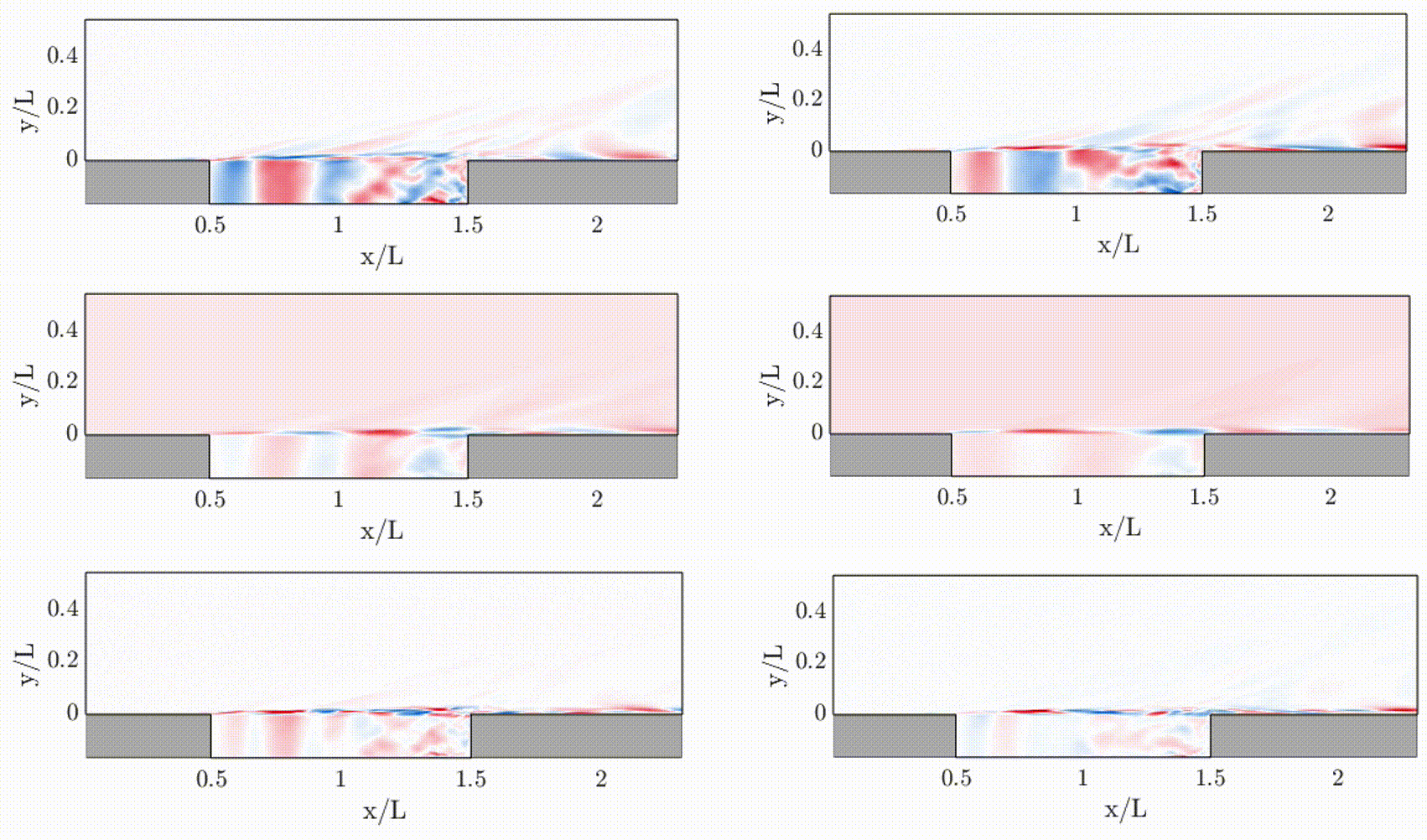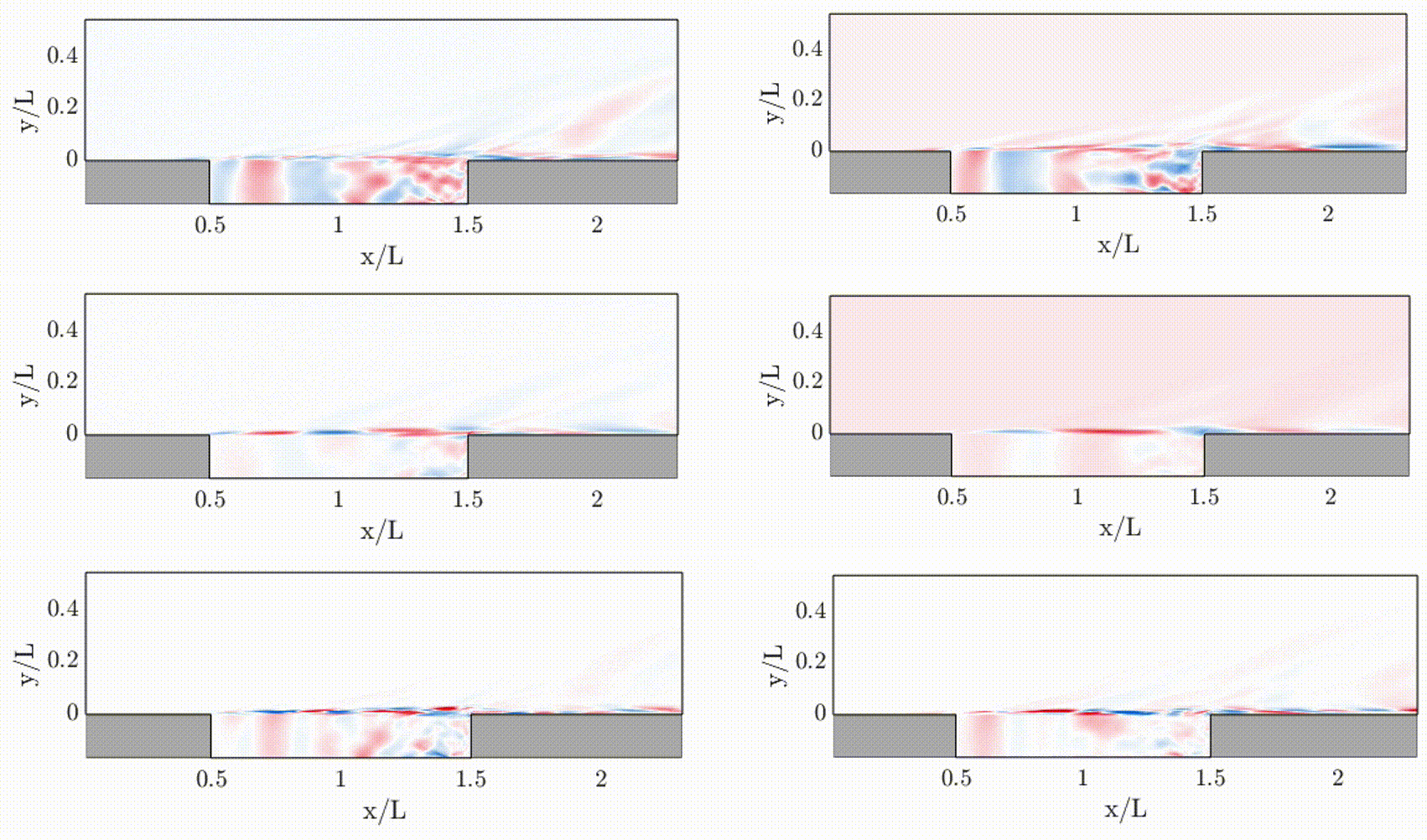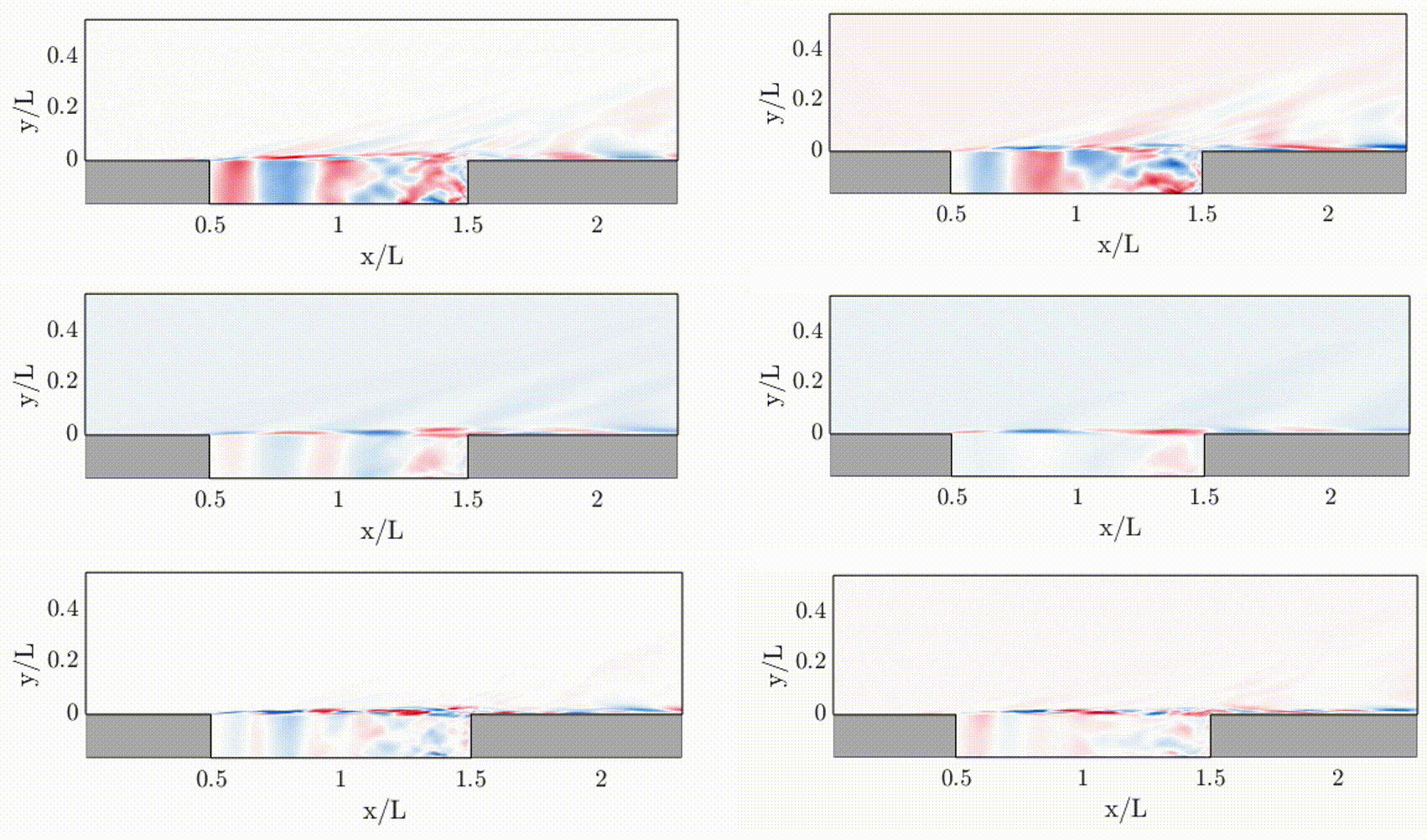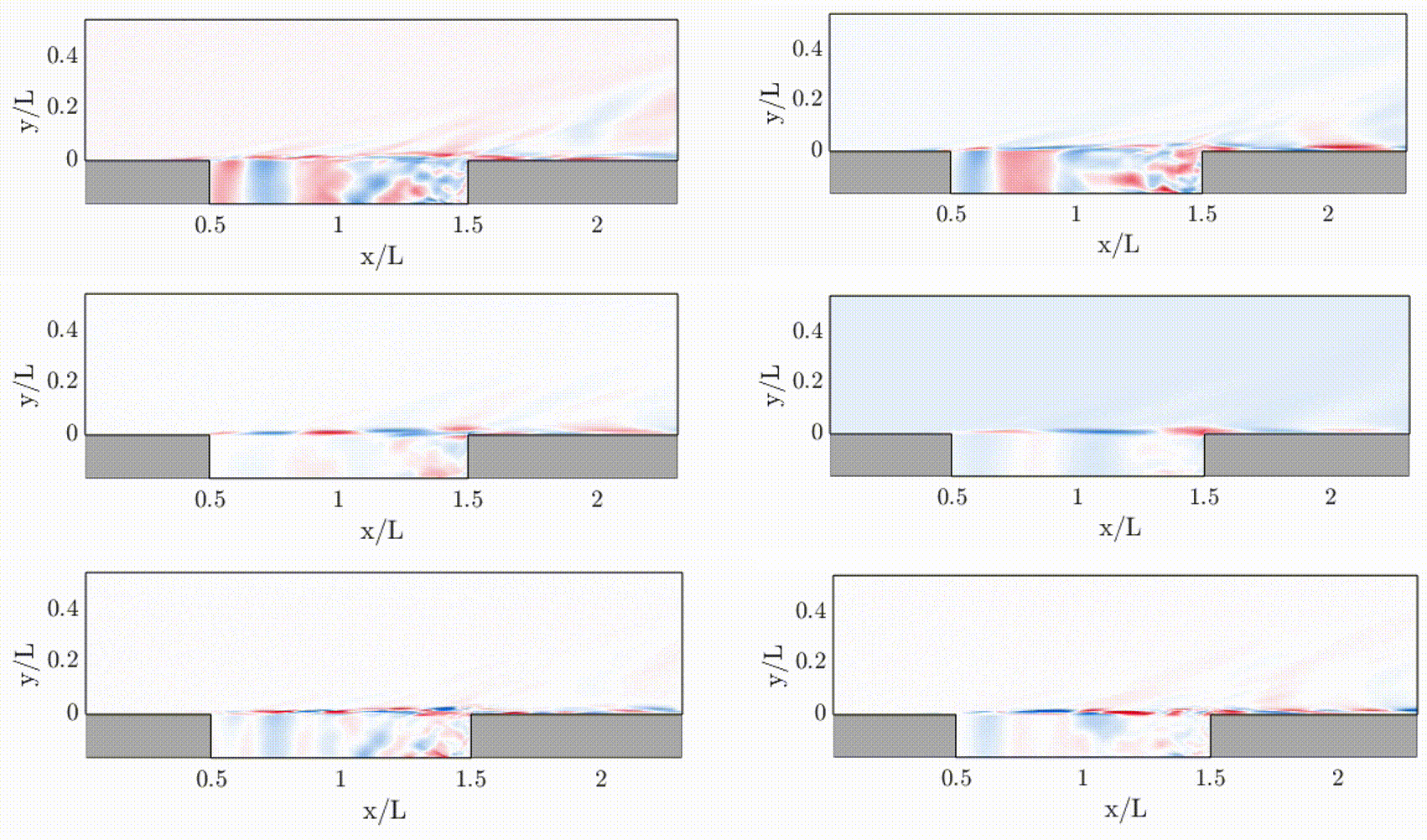
Modal analysis has been a standard and fundamental technique for the characterization, understanding, and modeling of dynamical systems, by extracting out physically-important spatial and temporal features. Modal analysis has been extensively applied to mechanical and structural systems, and is also recently becoming common practice in the analysis of, e.g., fluid dynamics and energy systems (such as power grids).
Modal analysis naturally extends to the Koopman operator theory, such that a nonlinear, spatiotemporally evolving, dynamical system can be (nearly) exactly transformed into a linear system. Such operator-theoretic techniques provide insights into the system dynamics in terms of stability, time scales, controllability/observability, etc., which are otherwise not easily attainable for nonlinear systems. Such insights can facilitate the discovery of unknown physical mechanisms hidden in the system, as well as inform the design of controllers for realistic engineering systems, such as aerial robots and power grids.
Currently we focus on the data-driven approaches based on the operator-theoretic techniques, with applications to an expanding list of engineering problems, including
- Hypersonic fluid-thermal-structural interaction problems (SciTech2022)
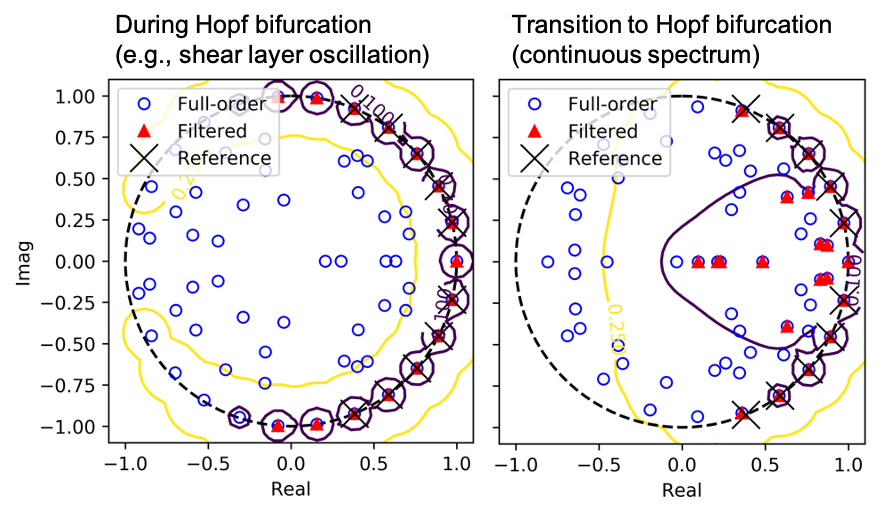
- Flow stability of high-speed shear layers (APS DFD22)
- Dynamics of power grid systems (paper, fund)
- Bayesian approach for spectral estimate of nonlinear dynamics (Aviation2023, ArXiv)
- Application to nonlinear aeroelastic analysis and control (SciTech2024)